Le format d’encodage du jeu One up

On m’a récemment montré ce nouveau jeu, dérivé du vénérable sudoku, nommé One up. Vous le trouverez sur le site officiel https://www.oneuppuzzle.com qui propose une nouvelle grille quotidiennement. Il existe également des applications android et iPhone.

Le principe est relativement proche de celui du sudoku. Je ne vous ferai pas l’affront d’expliquer les règles de ce dernier. Par contre, je vais expliquer un peu celles de One up.

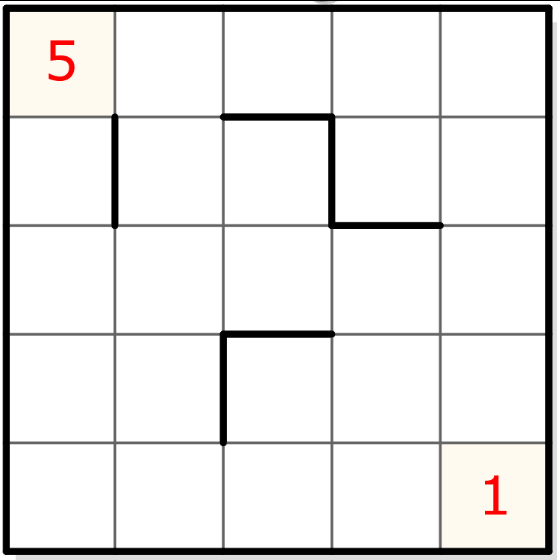
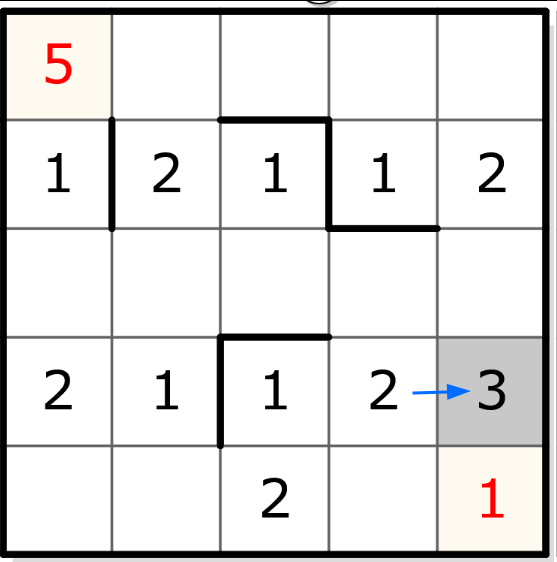
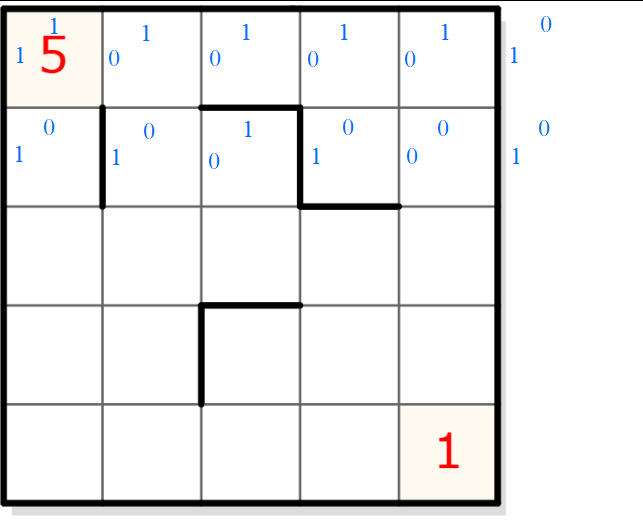
Pour cela, prenons l’exemple d’une grille simple de 5×5 :

Les règles

Il s’agit de remplir chaque case non encore occupée avec un chiffre dont la valeur ne peut apparaître qu’une fois par segment de ligne et par segment de colonne, de 1 à la taille du segment mais, évidemment, pas nécéssairement dans cet ordre. Un segment est une série de cases (en ligne ou en colonne) délimitées par un trait en gras et les bords de la grille.

La notion de carré de 3×3 du sudoku n’existe plus et a été remplacée par cette logique de segments qui engendre des types de déductions différents, même si le style est malgré tout très proche du sudoku.

Exemples de déductions

Un segment de taille 1 (par exemple, celui, horizontal, de la 2ème ligne, 1ère colonne) contiendra donc forcément le chiffre 1 :

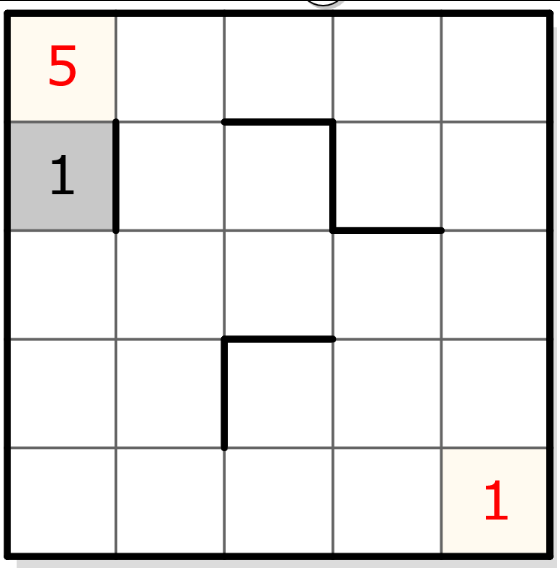
On peut ensuite faire des déductions sur les segments de taille 2 en suivant une logique d’exclusion :

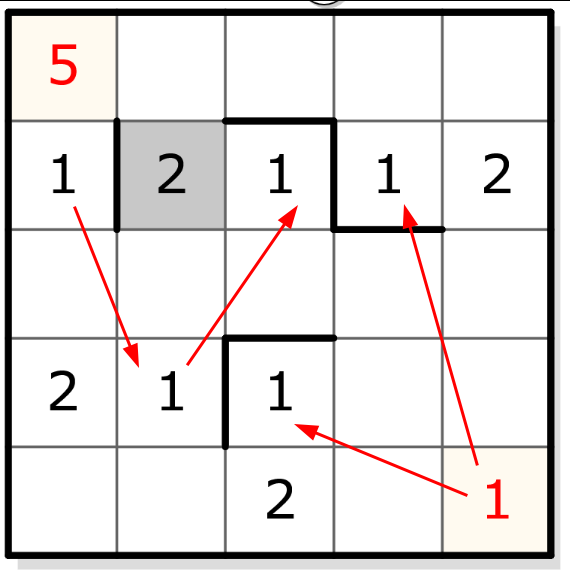
Et ainsi de suite. Les déductions se propagent et on devrait finir par pouvoir remplir toute la grille de cette façon. Par exemple, dans un segment de taille 3, le “1” est déjà occupé et le “2” ne peut plus être que dans la case dont le segment vertical n’a pas encore de “2”:

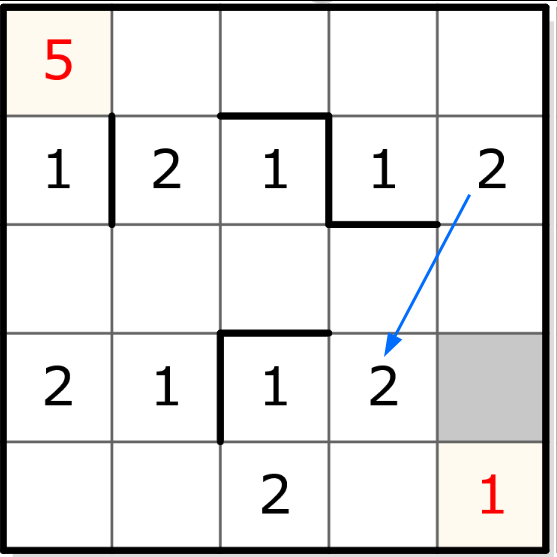
Ce qui implique directement la présence du “3” dans le segment horizontal :

Défauts du site officiel et de l’appli

J’ai rapidement attrapé le virus. Je joue actuellement tous les jours et j’essaye d’améliorer mes temps (le jeu est chronométré) pour tenter de battre la personne qui m’a fait découvrir le jeu (c’est pas gagné 😅).

Cependant, j’ai vite été déçu par le peu de possibilités de s’entrainer avec les sites et applications officielles (l’application officielle coûte 5€). À l’heure où j’écris cet article, sur le site officiel, nous en sommes au puzzle quotidien #274 or il y est impossible d’accéder ni de jouer aux 273 puzzles passés. Certes, on a accès à quelques grilles d’entrainement, mais ça ne va pas bien loin. De plus, il n’est pas non plus possible de rejouer la grille du jour.

J’ai pensé que ces fonctionnalités pouvaient être monétisées et j’ai acheté l’application android sans trop réfléchir (c’est tout moi), quelle n’a pas été ma surprise de découvrir que…

1. Les grilles passées ne sont pas listées là non plus. On peut jouer sur 10 grilles de chaque taille, de 5×5 jusqu’à 10×10, soit 50 grilles en tout. Aucune idée du lien entre ces grilles et les 274 grilles qui sont déjà tombées. Globalement, tout cela m’a l’air un peu opaque sans justification valable.
2. L’application est buggée sur la gestion du temps de résolution et de la pause : si vous finissez une grille en deux minutes mais que vous avez mis la pause pendant dix minutes au milieu, le jeu vous félicite d’avoir fini la grille en douze minutes 😐
3. L’application et le site ne sont pas très ergonomiques sur mobile. On doit péniblement scroller sur la liste des grilles pour atteindre celles qu’on n’a pas encore remplies. Et puis dans le jeu lui-même, les chiffres sont situés sous la grille et même si on peut s’y habituer, il me paraîtrait plus pertinent d’avoir, par exemple, les chiffres disponibles qui apparaissent sous le doigt avec un genre de menu contextuel et/ou un mouvement de swipe. Cela dit, cette approche pourrait amener son lot de soucis (on peut vouloir cliquer sur une case sans déclencher la popup). À voir.

En tout cas, pour 5€, je trouve ça plutôt léger.

Il n’en a pas fallu davantage pour que ma fibre de developpeur soit tilillée. J’ai donc entrepris de recréer ma propre implémentation de One up et de résoudre ces soucis. J’ai déjà une première version très brouillon du jeu en place :

Mais maintenant que je dois implémenter la gestion des séparateurs de segments, la question de l’encodage d’une grille, autrement dit comment elle est stockée et convertie en partie concrètement jouable, vient au premier plan. C’est ce processus de recherche du format officiel d’encodage d’une grille qui a motivé l’écriture de cet article.

Découverte du format d’encodage

Plutôt que d’inventer mon propre modèle de stockage, je me suis dit qu’il vaudrait mieux pouvoir tirer partie du mode de stockage du site officiel pour pouvoir extraire plus facilement les puzzles auxquels j’aurais accès. Ce serait toujours ça de gagné.

Retrouver le format de stockage d’une grille

Pour retrouver le format officiel, direction le site One up, en particulier une grille d’entrainement par exemple, puis ouverture de la console développeur (navigateur Chrome).

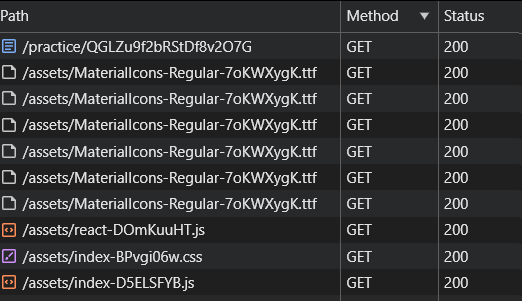
Premier constat, l’application se charge d’un coup sous la forme d’un document HTML, JS et CSS (grosso modo 4 requêtes HTTP), quelques polices de caractères, des requêtes vers les systèmes de Google et c’est à peu près tout. Aucune API Web ne semble interrogée a posteriori qui permettrait de recevoir une grille sous forme de données exploitables directement et ressemblant à une forme sérialisée d’une grille de jeu. La page HTML elle même ne contient aucune info, ce qui est typique des applications “Single page app” (ici ReactJs) où le premier document HTML ne sert que de coquille vide à l’application JS ; il va donc falloir aller creuser dans la seule information disponible : le script JS lui-même.

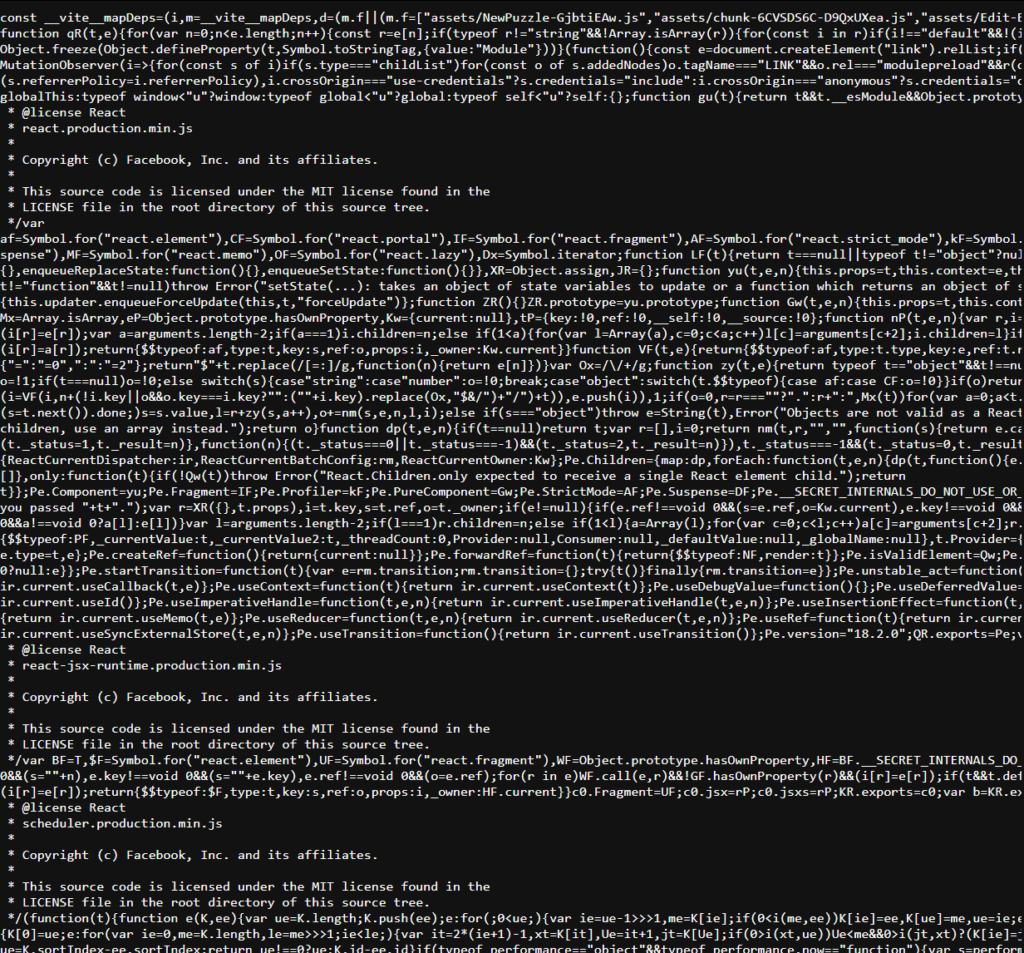
Ce beau fichier (dont le format est ce qu’on appelle “minifié”, c’est à dire complètement compacté pour prendre moins de place) est gigantesque. Je suppose qu’il contient a minima la bibliothèque ReactJS et a priori vers la fin, du code “métier”, c’est à dire le code de l’application One up elle-même.

En effet, en scrollant tout en bas de ce script, on aperçoit des données intéressantes :

Petite parenthèse, chaque grille du site officiel est affublée d’un identifiant, par exemple celui de mon exemple plus haut est “QGLZu9f2bRStDf8v2O7G”, accessible à tous depuis https://www.oneuppuzzle.com/practice/QGLZu9f2bRStDf8v2O7G. Dans le script, dont je me suis permis d’extraire le morceau intéressant et de le remettre en forme, on peut voir que les données de cette grille et de tous les autres puzzles d’entraînement sont directement exposés dans un tableau en “clair” :

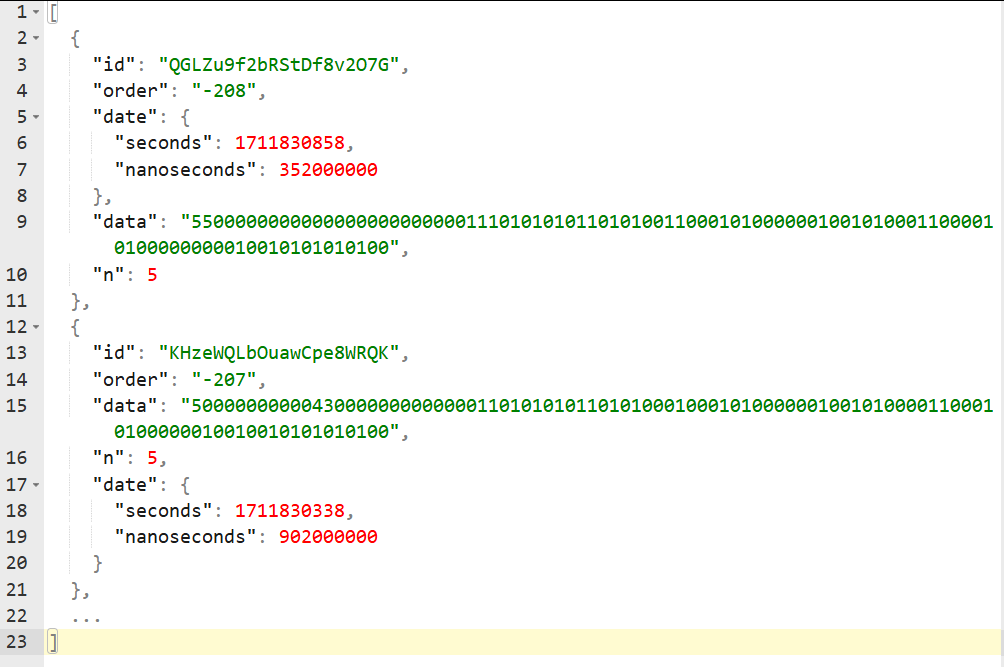
On tient le bon bout. Premièrement, on a la propriété “id”, qui donne directement l’identifiant de la grille ce qui est pratique pour nous y retrouver et recouper avec ce que l’on observe en tant qu’utilisateur. De plus, on constate, pour les deux grilles, que sont fournis le “n”, à savoir la taille de la grille (en l’occurence 5) et une chaîne de caractères “data” pour l’instant plutôt mystérieuse.

Deuxième partie : analyse du format de stockage

Les valeurs préexistantes

Comme je l’ai déjà évoqué, c’est cette analyse du champ “data” qui m’a motivé à écrire cet article. Il s’agit d’un processus que je trouve passionnant qu’on appelle communément “reverse ingeneering”. Il s’agit de comprendre une donnée, un format, sans davantage d’information que la donnée elle-même. Un peu comme un détective qui décrypterais une scène de crime pour résoudre une enquête.

La personne qui a développé ce format n’avait, à ma connaissance, pas prévu d’en partager la documentation. Il faut donc se retrousser les manches pour tenter de comprendre comment on passe de ça :

55000000000000000000000001110101010110101001100010100000010010100011000010100000000010010101010100

à ça :

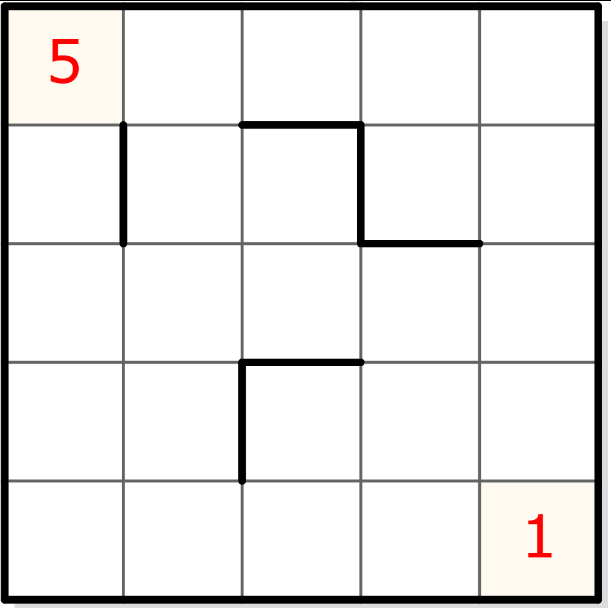
Avant de lire la suite, vous pouvez essayer par vous-même !

En tout cas, à partir de maintenant, je vais essayer de décrire chaque étape de mon analyse, y compris les fausses pistes car l’important, ce n’est pas la destination, mais le voyage ♥ 🤗.

Tout d’abord, je constate que l’encodage commence par “55” suivis de nombreux 0. L’intuition dit rapidement que les 0 correspondent sans doute aux cases vides dans le cadre de la description des chiffres “préexistants” de la grille (les chiffres “5” et “1” en rouge). Mais ce “5” est écrit deux fois ce qui me gène car il n’y a qu’un seul “5” à la première case (merci, Captain Obvious). Faudrait-il en déduire que chaque chiffre est présent deux fois dans le format, peut-être une fois pour décrire les lignes et une fois pour les colonnes ? Hmm… pas très efficace tout ça. Creusons un peu plus.

Si je compte le nombre de “0”, j’en trouve 23 avant le premier “1”. Cela correspond au nombre de cases vides entre le 5 et le 1 si on balaye la grille ligne par ligne. Cela confirme le fait que chaque valeur préexistante (“5”, “1” ou vide) est bien écrite une seule fois (j’ai envie de dire, heureusement !). Mais alors, pourquoi est-il écrit “5” deux fois ?

Comme nous avons la chance d’avoir d’autres grilles à disposition, servons-nous de la deuxième disponible. Nous pourrons probablement extraire quelque chose sachant qu’elle ne contient pas de “5” préexistant :

50000000000430000000000000110101010110101000100010100000010010100001100010100000010010010101010100

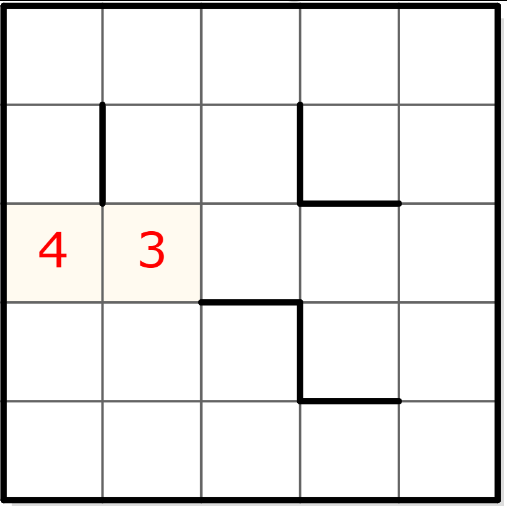
Ah ! On y voit plus clair ! Il y a toujours un “5”, une suite de 10 “0”, puis le “4” suivi du “3”, puis une série de 13 “0”. Le premier “5” réfèrerait donc manifestement à la taille de la grille ? C’est étrange car la taille de la grille était déjà présente par ailleurs, dans le tableau extrait du script JS. Souvent en développement, on évite ce genre de redondance. Cependant, si le champ “data” contient cette information, c’est peut-être que le développeur avait en tête d’utiliser cette chaine de caractère comme moyen d’échange unique pour passer des grilles, par exemple directement dans l’URL du site. Mais passons. Nous pouvons vérifier que la taille est bien spécifiée également dès le début dans l’encodage d’une grille de 8×8 :

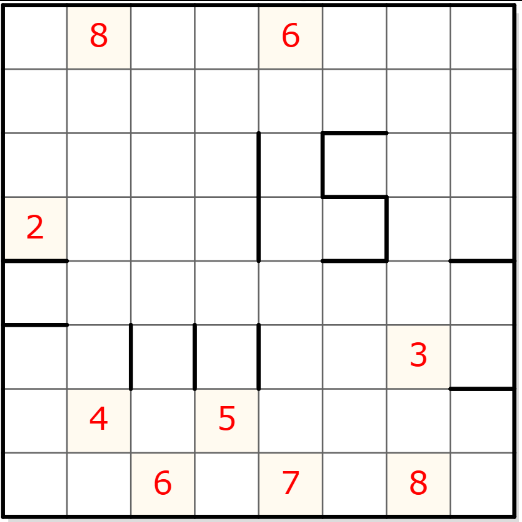
80800600000000000000000002000000000000000000000300405000000607080110101010101010110100000000000000010100000001011000010100000001001100010110000000001000110110010101000000010100000000000000110100000000000000010010101010101010100

En effet, l’encodage commence donc toujours bien par la taille de la grille.

Petite parenthèse : on peut se poser la question des grilles 10×10 (dont on trouve des exemples dans l’application) : vu que le nombre 10 fait deux caractères, il va falloir envisager un traitement particulier si l’encodage commence par “1” en excluant bien sûr les grilles de 1×1.

Tout est donc logique pour (le début de) la liste des chiffres préinscrits dans la grille : après un caractère précisant la taille N de la grille, on a la liste de ces NxN chiffres dans l’ordre, ligne par ligne. Dans la grille 8×8, il y a en effet 64 caractères correspondant bien à l’image de la grille. Et dans notre premier exemple de grille 5×5, il y en a bien 25, formattés pour la lisibilité ici :

50000
00000
00000
00000
00001

Mais maintenant, comment interpréter la suite des chiffres de l’encodage ?

Les séparateurs de segments

Première hypothèse : quatre bits par cellule

Reprenons notre premier exemple en excluant ce que nous avons déjà analysé et compris (c’est à dire la taille puis les valeurs préexistantes):

110101010110101001100010100000010010100011000010100000000010010101010100

Il s’agit d’une suite de bits dont nous n’avons aucune façon de savoir a priori s’il s’agit d’un encodage standard ou d’un format spécifique. Une chose est presque sûre, pas complètement, on va voir, honnêtement, j’en mettrais pas ma main à couper mais un peu quand même… cette longue suite de bits fait “forcément” référence, d’une manière ou d’une autre, à la façon d’agencer les séparations de segments. Je mets “forcément” entre guillemets car je ne verrais pas d’autre information pertinente à stocker de toute façon. Cependant, ne connaissant pas tous les tenants et aboutissants du format de stockage, je ne peux pas en être certain : il n’est pas encore exclus que le format stocke, je ne sais pas moi, la taille des traits, la couleur des chiffres préexistants, etc. Tout est possible, même des choses pas forcément pertinentes car on ne sait pas ce qui se passait dans la tête du concepteur.

Partons cependant de cette hypothèse qu’au moins au début, les bits portent l’information des séparateurs de segments : on peut donc d’ores et déjà partir du principe que les “0” réfèrent à l’absence d’un séparateur et que les “1” réfèrent à leur présence. Mais comment cela est-il organisé ?

Nous pouvons par exemple partir du postulat que chaque cellule est décrite en terme de séparateurs par quatre valeurs “0” ou “1”, correspondant à ce schéma, en codant dans le sens des aiguilles d’une montre et en partant intuitivement de l’arrête de gauche, à savoir “1000” :

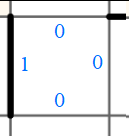
Autre exemple, “0110” :

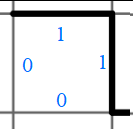
Cela voudrait dire que dans notre exemple, la première cellule devrait être décrite “1100”:

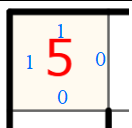
Or, ce n’est pas le cas. Le premier groupe de 4 bits est “1101”. Perdu.

De toute façon, ce ne serait pas très efficace de coder 4 bits par cellule pour ses 4 arrêtes, vu qu’en passant aux cellules suivantes avec ce codage, on répéterait l’information des arrêtes adjacentes. Comme dirait un collègue : “insight is 20/20, right” ?

Deuxième hypothèse : deux bits par cellule

Il me semble qu’il suffirait plutôt pour chaque cellule de stocker seulement deux bits, intuitivement l’arrête de gauche et celle du haut, ici “1001” pour deux cellules :

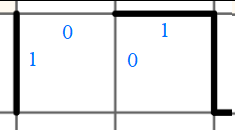
La ligne du dessous remplirait ainsi la fonction d’établir les séparateurs du bas de cette ligne là.

Si on vérifie ce format avec notre première grille, on devrait donc pouvoir faire correspondre dix bits par ligne (deux bits pour cinq cellules) avec ce que l’on observe sur la grille. Reformatons donc notre suite de bits par lignes de dix bits:

1101010101
1010100110
0010100000
0100101000
1100001010
0000000010
0101010101
00

Je remets ici la grille réelle pour rappel :

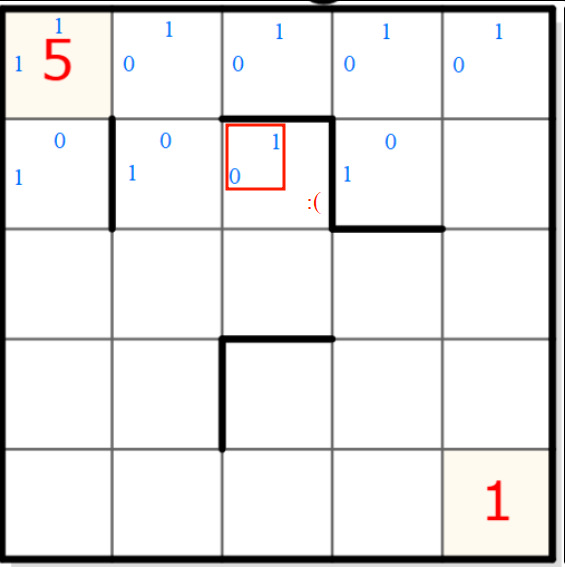
Mis à part le fait qu’on se retrouve avec trop de lignes et la dernière beaucoup trop courte, pour la première ligne, ça colle bien. Le format considère les arrêtes du pourtour de la grille comme des séparateur de segment, ce qui se tient. On sent qu’on se rapproche de quelque chose.

Cependant, à la deuxième ligne, troisième cellule, ça ne colle plus. Le codage donne “10” alors que c’est l’arrête du haut qui a un séparateur, le codage devrait donc être “01” comme sur l’image.

Et puis, je ne l’ai pas précisé, mais il me reste un tas de bits en trop à la fin qui me dérangent car je ne vois pas à quoi ils pourraient faire référence (même si, comme je l’ai déjà dit, cela pourrait encoder autre chose dont je n’ai pas conscience). Il y a anguille sous roche !

Une petite chose me chagrine dans cette dernière hypothèse, c’est que les séparateurs “externes”, c’est à dire du bord de la grille, sont spécifiés pour l’arrête de gauche et celle du haut, mais pas pour celle de droite, car en spécifiant la dernière cellule de la ligne, le codage ne donne pas d’info pour l’arrête de droite. Cela n’est pas très grave en théorie car on sait que la grille fait cinq cellules de large et que la grille est forcément délimitée à droite.

Sauf que cette hypothèse est manifestement fausse d’une part et d’autre part, le bon format permet a priori de générer le dessin dans le site officiel (technologie SVG). Il faudrait peut-être donc considérer que l’arrête de droite est également encodée ?

Essayons d’imaginer qu’au lieu d’encoder cinq cellules en terme d’arrêtes, nous encodions plutôt six paires d’arêtes, un peu comme ça :

Vérifions cela en regroupant nos bits, non plus par groupe de dix, mais par groupes de douze.

110101010110
101001100010
100000010010
100011000010
100000000010
010101010100

Cette fois-ci, c’est bon ! On constate d’abord que le format encode des cellules imaginaires à droite et en bas afin, en quelque sorte, d’inclure toutes les arrêtes à dessiner de la grille, mais de plus, que tous les bits ont finalement été utilisés.

A posteriori, je ne suis pas certain que j’aurais procédé de cette manière si j’avais dû encoder le format de la grille. En effet, je ne trouve pas nécéssaire de spécifier les arrêtes externes. Cependant, l’exercice m’a beaucoup plu et je vais pouvoir maintenant continuer mon implémentation du jeu en exploitant ce format d’encodage 😎

À bientôt !